基于栈实现算术表达式的解析与运算

算术表达式作为最常用的逻辑运算的写作方式，是一种易用，易理解的规则和数据的组合体。这种组合体对于人来说，理解其中的规则，既可以快速计算出结果，但是在代码中，不同操作符的优先级使得对于算术的字符读取无法按照常规的逐行逐句读取，需要在读取的同时，结合上下文来动态的判断优先级，并进行打标来处理，这种方式会导致频繁的上下文切换和跨字符读取，严重拖慢执行数据。基于此，可以采用后缀表达法来预处理算术表达式。

后缀表达式转换

算式分解

对于一般算式来说，其主要可以分为三部分，分别为 操作符，操作数，操作值，其中：

• 操作数：即为算式中的需要计算的数，可以为乘数，也可以为除数等，一切由后续的操作符来定义。
• 操作符：即为算式中的计算标识，标识操作数按照何种方式进行组合，同时也定义操作的优先级。
• 操作值：即为算式中计算的结果值，作为操作数在操作符不同规则下组合的产物。

  tips：在多级运算中，有时候操作值也会转换为操作数，继续参与接下来的运算。

后缀表达式说明

在说后缀表达式之前，可以先理解下中缀表达式；

• 中缀表达式：即我们日常看到的算法模式，形如 a * (b + c) 这种模式，所有的符号按照执行顺序进行排列，可以很方便的明白其中的规则并进行计算。
• 后缀表达式：即将中缀表达的格式按照实际计算的优先级，将操作符进行后置排列，例如 abc+* 这种模式，完全排除括号对计算优先级的处理，可以满足计算中逐句读取，逐句解析，逐句计算的要求。

在理解后缀表达式之后，就可以发现这种表达方式在计算机处理中的高效之处，以及其设计的巧妙，合理的解决了括号带来的优先级跳跃的问题和依赖上下文处理的性能损耗问题。以下有部分中缀和后缀表达式的对比，可以先体会下其中的设计思路：

中缀表达式	后缀表达式
A+B-C	AB+C-
A*B/C	AB*C/
A+B*C	ABC*+
A*B+C	AB*C+
A*(B+C)	ABC+*
A_B+C_D	AB_CD_+
(A+B)*(C-D)	AB+CD-*
((A+B)*C)-D	AB+C*D-
A+B*(C-D/(E+F))	ABCDEF+/-*+

转换规则

针对不同的算式表达式，在从中缀表达式转换为后缀表达式时，需要遵循一下规则：

• 所有的操作数按照顺序进行排列（不改变中缀算式的操作数排列规则）
• 遇到操作符时，如果可以直接进行运算的，则将操作符复制到两个操作数后面
• 遇到括号这种能够提升优先级的操作符，需要将当前操作符先搁置，待到后续优先级升级的算式操作转换完成后，再将当前操作符复制到后面。

转换实例

下面来看几个简单的算式的转换过程

第一个是 A + B -C 的转换方式

从中缀字符串中读取字符串	分解中缀表达式过程	求后缀表达式过程	说明
A	A	A
+	A+	A	读到+，无法运算 搁置
B	A+B	AB
-	A+B-	AB+	读到-，可以运算，则可以把+复制到后缀字符串中
C	A+B-C	AB+C
END	A+B-C	AB+C-	当读到表达式结尾处，可以复制-

第二个是 A + B * C 的转换方式

从中缀表达式中读取字符串	分解中缀表达式过程	求后缀表达式过程	说明
A	A	A
+	A+	A	读到+，无法运算 搁置
B	A+B	AB
*	A+B*	AB	读到*，无法运算 搁置
C	A+B*C	ABC
	A+B*C	ABC*	看到C,可运算后可以复制*
END	A+B*C	ABC*+	看到表达式末端时，可以复制+

第三个是 A * ( B + C ) 的转换方式

从中缀表达式中读取字符串	分解中缀表达式过程	求后缀表达式过程	说明
A	A	A
*	A*	A	读到*，无法运算 搁置
(	A*(	A	读到(，不能复制
B	A*(B	AB
	A*(B+	AB
+	A*(B+C	ABC	不能复制+
C	A*(B+C)	ABC+	看到）时，可以运算，可以复制+
)	A*(B+C)	ABC+*
END	A*(B+C)	ABC+*	看到表达式末端时，可以复制*

算法设计思路

通过以上简单应用的转换，可以看到，操作数的排列是不用改变的，只有操作符是发生了顺序的变化，同时操作符也需要受到优先级高低的影响，因此在转换过程中，可以考虑使用栈这个结构，将每一个操作符与前一个对比，根据优先级高低，来处理操作符入库或者是复制的操作。

tips: 特别，在转换的过程中，会出现 数值的顺序的颠倒，例如 A/B ，会变为 AB/ ，在栈的结果中，在计算的时候，需要注意减法和除法的值的使用问题。

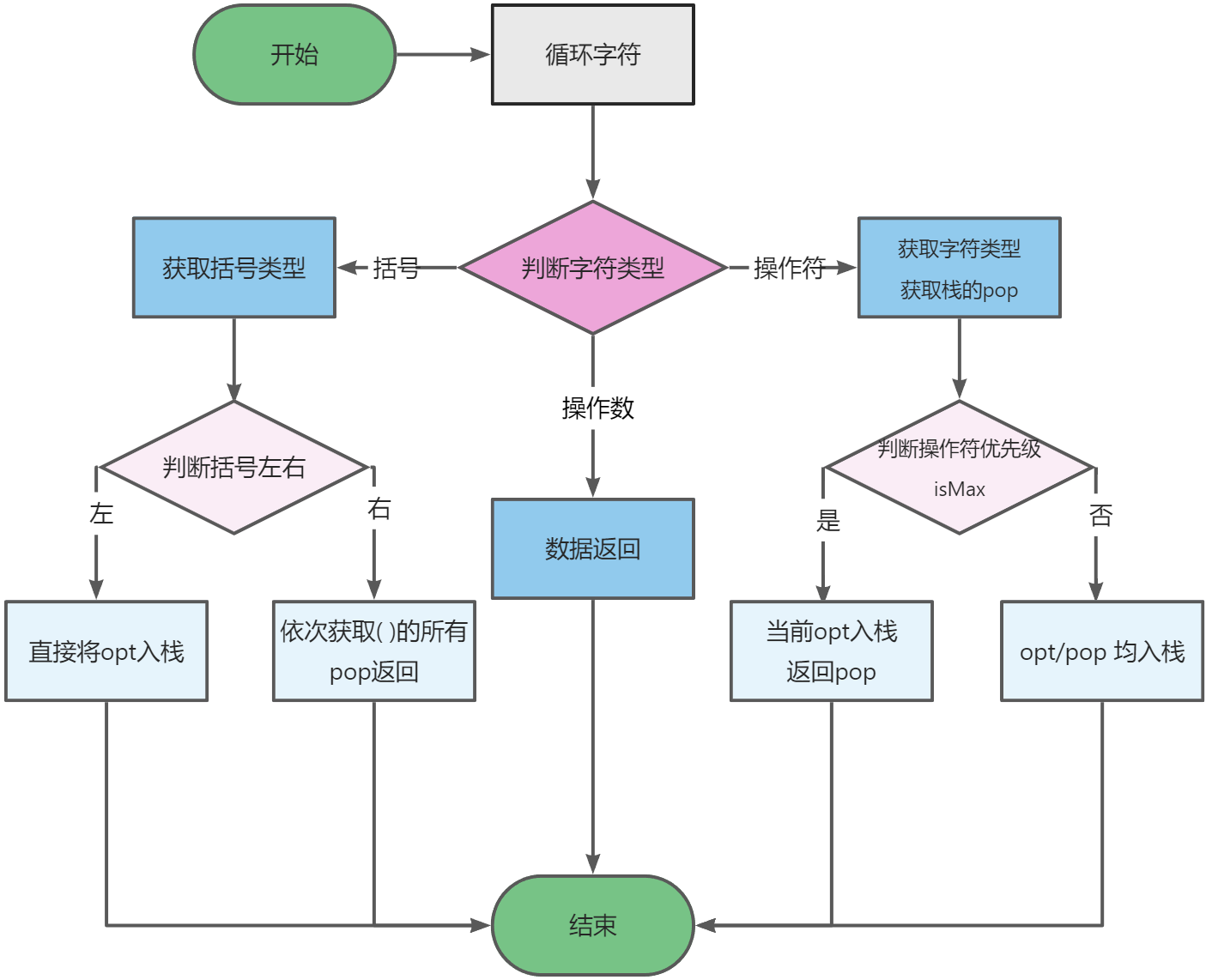
代码实现

/** 在做后缀解析的过程中，保存操作符 */
private static final Stack<String> SYMBOL_STACK = new Stack<>();
/** 表明符号列表 */
private static final List<String> DEFAULT_SYMBOL_LIST = Lists.newArrayList("+","-","*","/");
private static final String LEFT_BRACKET = "(";
private static final String RIGHT_BRACKET = ")";

private static String convert(String opt){
    if(opt == null){
    	return "";
    }
    // 判断数据类型
    if(DEFAULT_SYMBOL_LIST.contains(opt)){
        // 当opt 为 操作符时
        // 如果栈为空，则直接将当前操作符入库
        if(SYMBOL_STACK.isEmpty()){
            SYMBOL_STACK.push(opt);
            return "";
        }
        String pop = SYMBOL_STACK.pop();
        // 如果 取出的 pop 即之前的操作符 优先级高于 当前opt 则表示当前操作数可以运算，则复制取出的操作符
        // 同时将当前操作符入栈
        if(isMax(pop,opt)){
            SYMBOL_STACK.push(opt);
            return pop;
        }else{
            // 如果 取出的pop 优先级低于 当前操作符，说明当前 结果不可运算 ，则 将取出的pop 和当前 opt均入栈
            SYMBOL_STACK.push(pop);
            SYMBOL_STACK.push(opt);
            return "";
        }
    
    }else if(LEFT_BRACKET.equals(opt) || RIGHT_BRACKET.equals(opt)){
        // 当opt 为 左右括号时
        if(LEFT_BRACKET.equals(opt)){
            // 左括号 ，则 当前无法计算 则直接将符号入栈即可
            SYMBOL_STACK.push(opt);
            return "";
        }else {
            // 右括号 即当前数据可以计算 ，取出 ) 之间所有入栈的 操作符均取栈顶复制到后面
            StringBuffer sb = new StringBuffer();
            while (!SYMBOL_STACK.isEmpty()){
                String pop = SYMBOL_STACK.pop();
                // 截止到 ( 之前的操作符，主要是解决在多重 (( 的情况下，只复制当前 ( ) 结构内的操作符
                if(pop.equals(LEFT_BRACKET)){
                    break;
                }
                sb.append(pop);
            }
            return sb.toString();
        }
    }else{
        // 操作数 直接按照顺序输出即可
        return opt;
    }
}

/** 
 * @description: 判断操作符的优先级
 * @date: Create in 2022/10/20 16:15
 */
private static boolean isMax(String max,String min){
    return SymbolEnum.getLevel(max) >= SymbolEnum.getLevel(min);
}

算式计算

在将算式从中缀表达式转换为后缀表达式之后，再想进行计算就及其的简单了。只需要将操作数不断的入栈，然后遇到操作符之后，从栈中取出两个数，进行计算，然后将操作值再入栈成为操作数，直到结束。以下直接展示代码实现。

• 不同符号计算的枚举类

  public enum SymbolEnum {
  
      ADD(1,"+"){
          @Override
          protected int calculate(int a, int b) {
              return a+b;
          }
      },
      SUB(1,"-") {
          @Override
          protected int calculate(int a, int b) {
              return a-b;
          }
      },
      MUL(2,"*") {
          @Override
          protected int calculate(int a, int b) {
              return a*b;
          }
      },
      DIV(2,"/") {
          @Override
          protected int calculate(int a, int b) {
              return a/b;
          }
      },
      LEFT(0,"(") {
          @Override
          protected int calculate(int a, int b) {
              return 0;
          }
      },
      RIGHT(0,")") {
          @Override
          protected int calculate(int a, int b) {
              return 0;
          }
      },
      ;
      private int level;
      private String symbol;
      SymbolEnum(int level, String symbol) {
          this.level = level;
          this.symbol = symbol;
      }
  
      // 不同符号实现的抽象方法
      protected abstract int calculate(int a, int b);
  
      // 对不同操作符进行数据运算
      public static int calculate(int a, int b, String symbol){
          for (SymbolEnum value : SymbolEnum.values()) {
              if(value.symbol.equals(symbol)){
                  return value.calculate(a,b);
              }
          }
          return 0;
      }
  
      // 获取符号的优先级
      public static int getLevel(String symbol){
          for (SymbolEnum value : SymbolEnum.values()) {
              if(value.symbol.equals(symbol)){
                  return value.level;
              }
          }
          return 1;
      }
  
  }

• 计算结果

  /** 在计算结果的时候，保存操作数及操作值 */
  private static final Stack<Integer> VALUE_STACK = new Stack<>();
  
  public static void main(String[] args) {
      String test = "(((1+1)-3)+4)*(6+2)";
      StringBuffer sb = new StringBuffer();
      for (int i = 0; i <= test.length(); i++) {
          if(i == test.length()){
              while (!SYMBOL_STACK.isEmpty()){
                  sb.append(SYMBOL_STACK.pop());
              }
              continue;
          }
          sb.append(convert(String.valueOf(test.charAt(i))));
      }
      String last = sb.toString();
      System.out.println(sb.toString());
  
      for (int i = 0; i < last.length(); i++) {
          calculate(String.valueOf(last.charAt(i)));
      }
      System.out.println(VALUE_STACK.pop());
  }
  
  
  /**
   * @description: 对解析后的数据进行计算
   * @date: Create in 2022/10/20 16:16
   */
  private static void calculate(String opt){
      if(DEFAULT_SYMBOL_LIST.contains(opt)){
          Integer b = VALUE_STACK.pop();
          Integer a = VALUE_STACK.pop();
          int calculate = SymbolEnum.calculate(a, b, opt);
          VALUE_STACK.push(calculate);
      }else {
          VALUE_STACK.push(Integer.parseInt(opt));
      }
  }

总结

基于栈的FILO的特性，在处理一些需要等待，而且需要保持整体顺序的算法中，具有着无与伦比的优势和非常大的普适性。

对于自然语言到机器语言的转换过程中，根据上下文的理解对于自然语言来说是非常简单的，但是机器语言中，最好是减少上下文的切换，减少逻辑块的优先级跳跃，才能更好的服务于编码和机器执行。

参考文献

CSDN

java使用栈解析算术表达式