基于RTree索引和射线法实现的电子围栏

电子围栏技术被广泛应用于地理围栏、安防监控、无人机限制飞行区域等领域。如何快速而准确地判断一个点是否在一个多边形区域内，是实现电子围栏的核心问题。在车联网场景下，需要用到大量的基于经纬度的电子围栏，特别是多边形围栏，基本上贯穿车辆监控和管理的整个生命周期，且其高频的定位聚焦到平台做云计算，会让简单的射线法消耗庞大的计算资源开销和造成实时积压，因此，反射法结合RTree算法进行粗筛成为高效判断是否在围栏的重要方式。

射线法

射线法（Ray Casting）是一种判断点是否在多边形内的经典算法。其基本原理是：从待判断点向任意方向引一条射线，计算该射线与多边形边界的交点数。如果交点数为奇数，则点在多边形内；如果交点数为偶数，则点在多边形外。

图形说明

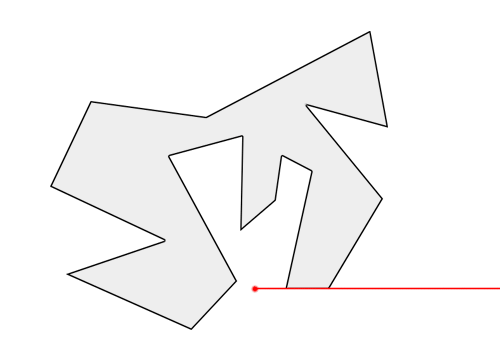
在如下图的一个不规律的多边形中，怎么判断这个点是不是在多边形内部 (😮‍💨别告诉我用肉眼观察……）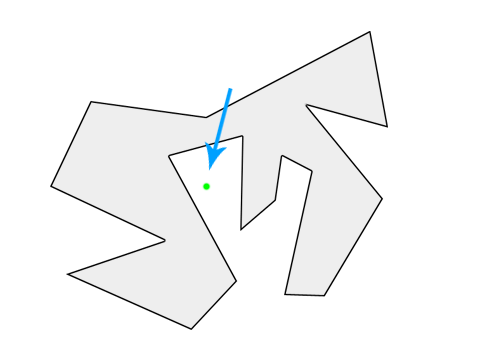

针对这个平面内任意闭合曲线，我们都可以直观地认为，曲线把平面分割成了内、外两部分，其中“内”就是我们所谓的多边形区域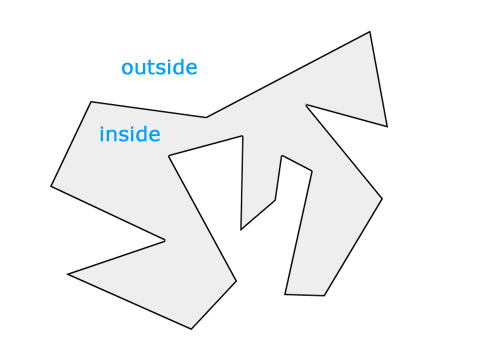

基于这一认识，对于平面内任意一条直线，可以有下面这些结论：

• 直线穿越多边形边界时，有且只有两种情况：进入多边形或穿出多边形。
• 在仅考虑二维平面的情况下，直线不可能从内部再次进入多边形，或从外部再次穿出多边形，即连续两次穿越边界的情况必然成对。
• 直线可以无限延伸，而闭合曲线包围的区域是有限的，因此最后一次穿越多边形边界，一定是穿出多边形，到达外部。

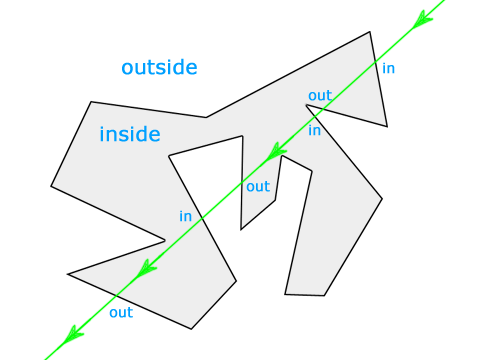
算法转换

• 当射线穿越多边形边界的次数为偶数时，所有第偶数次（包括最后一次）穿越都是穿出，因此所有第奇数次（包括第一次）穿越为穿入，由此可推断点在多边形外部。
  
• 当射线穿越多边形边界的次数为奇数时，所有第奇数次（包括第一次和最后一次）穿越都是穿出，由此可推断点在多边形内部。
  
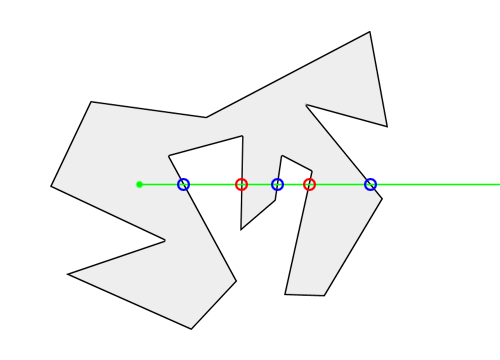
• 当点在多边形的线上或者与多变形顶点重合时，通过计算点与两个多边形顶点的连线斜率是否相等即可

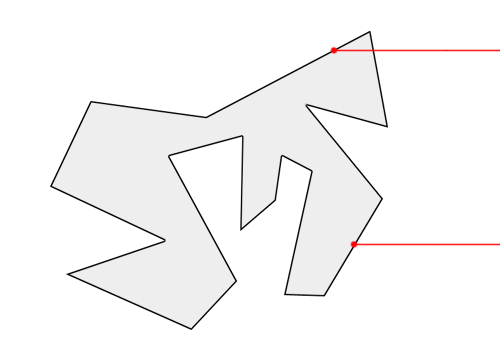
• 当点连续经过了多边形的两个相邻顶点，即射线平行于多边形的一条边，可以通过射线连续经过的两个顶点如果都位于射线以上的一侧，因此这种情况看作没有发生穿越就可以

算法实现

import java.util.List;

public class PolygonFence {
    private List<Point> vertices;

    public PolygonFence(List<Point> vertices) {
        this.vertices = vertices;
    }

    public boolean isInside(Point point) {
        int intersectCount = 0;
        for (int i = 0; i < vertices.size(); i++) {
            Point start = vertices.get(i);
            Point end = vertices.get((i + 1) % vertices.size());
            if (isRayIntersectsSegment(point, start, end)) {
                intersectCount++;
            }
        }
        return (intersectCount % 2) == 1; // 奇数表示在多边形内
    }

    private boolean isRayIntersectsSegment(Point point, Point start, Point end) {
        double px = point.getLon();
        double py = point.getLat();
        double sx = start.getLon();
        double sy = start.getLat();
        double ex = end.getLon();
        double ey = end.getLat();

        // 边平行于x轴，不相交
        if (sy == ey) {
            return false;
        }

        // 点在边的上方或下方
        if (py < Math.min(sy, ey) || py > Math.max(sy, ey)) {
            return false;
        }

        // 计算交点的x坐标
        double xIntersect = sx + (py - sy) * (ex - sx) / (ey - sy);

        // 交点在点的右边
        return xIntersect > px;
    }
}

RTree索引

RTree 是一种广泛应用于空间数据索引的数据结构。它通过将空间数据（如点、矩形等）组织成树形结构，支持快速的区域查询和邻近查询。RTree 的节点分为叶节点和内部节点，叶节点存储实际的数据对象，内部节点存储子节点的最小外包矩形（MBR, Minimum Bounding Rectangle）。

为什么用RTree索引

当地理围栏多边形数目较少时，我们可以依次遍历每一个多边形（暴力遍历法），然后用射线法进行判断，这样效率也很高。而当多边形数目较多时，比如有10万个多边形，这个时候需要执行10万次射线法。暴力遍历法效率低下的原因是与每一个多边形都进行了射线法判断，如果能减少射线法的调用次数性能就能提升。因此引入Rtree索引通过粗筛的方法快速找到符合条件的少量多边形，然后对粗筛后的多边形使用射线法判断，这样射线法的执行次数大大降低，效率也能大大提高。

💡对于一维数据我们常常使用索引的方法，比如通过B树索引找到某一个范围区间段，然后对此范围区间段进行遍历查找，对于二维空间数据常常使用空间索引的方法，比如通过R树找到范围区间内的多边形，然后对此范围内的多边形进行精确判断

RTree算法思路

• 构建多边形的最小外包矩形（MBR）并用 RTree 进行索引

💡核心是获取多边形最大的x,y轴坐标，并构建最小外包矩形

• 将 MBR 划分为多个子矩形，并存储到 RTree 中

💡多个mbr会有一定的交集，这个正常是被允许的，因为在构建多边形的mbr过程中，会有一点的空间扩充

• 使用射线法对 RTree 中的子矩形进行过滤，快速判断点是否在多边形内

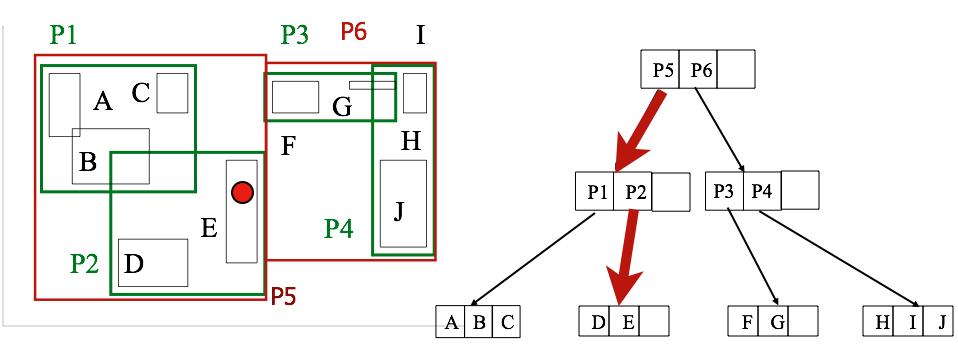
💡查询流程：

• 首先通过R树迅速判断用户所在位置（粗红点）是否被外包矩形覆盖（红色点代表用户所在位置；R树平均查询复杂度为O(Log(N))，N为多边形个数）；
• 如果不被任何外包矩形覆盖则返回不在地理围栏多边形内；
• 如果被外包矩形覆盖则还需要进一步判断是否在此外包矩形的多边形内部，采用上文提到的射线法判断。

算法实现

• 导入maven依赖

  <!-- https://mvnrepository.com/artifact/com.github.davidmoten/rtree -->
  <dependency>
    <groupId>com.github.davidmoten</groupId>
    <artifactId>rtree</artifactId>
    <version>0.8.7</version>
  </dependency>

• 构建RTree

  import com.github.davidmoten.rtree.Entry;
  import com.github.davidmoten.rtree.RTree;
  import com.github.davidmoten.rtree.geometry.Geometries;
  import com.github.davidmoten.rtree.geometry.Rectangle;
  import io.reactivex.Observable;
  
  import java.util.ArrayList;
  import java.util.List;
  
  public class PolygonFence {
      private String name; // 多边形ID或名称
      private String code; // 行政编码
      private List<Point> vertices; // 多边形的顶点列表
      private RTree<Edge, Rectangle> rTree; // R树索引
      private Rectangle boundingBox; // 多边形的最小外包矩形
  
      public PolygonFence(String name, String code, List<Point> vertices) {
          this.name = name;
          this.code = code;
          this.vertices = vertices;
          this.rTree = RTree.create();
          initializeRTree(vertices);
          calculateBoundingBox(vertices);
      }
  
      // 构建rtree索引
      private void initializeRTree(List<Point> vertices) {
          List<Edge> edges = createEdgesFromVertices(vertices);
          for (Edge edge : edges) {
              Rectangle rectangle = Geometries.rectangle(
                      Math.min(edge.x1, edge.x2), Math.min(edge.y1, edge.y2),
                      Math.max(edge.x1, edge.x2), Math.max(edge.y1, edge.y2)
              );
              rTree = rTree.add(edge, rectangle);
          }
          // 调试信息：打印所有的边
          System.out.println("All edges added to RTree:");
          edges.forEach(System.out::println);
      }
      
      // 构建 mbr
      private void calculateBoundingBox(List<Point> vertices) {
          double minX = Double.MAX_VALUE, minY = Double.MAX_VALUE;
          double maxX = Double.MIN_VALUE, maxY = Double.MIN_VALUE;
  
          for (Point vertex : vertices) {
              if (vertex.getLon() < minX) minX = vertex.getLon();
              if (vertex.getLat() < minY) minY = vertex.getLat();
              if (vertex.getLon() > maxX) maxX = vertex.getLon();
              if (vertex.getLat() > maxY) maxY = vertex.getLat();
          }
  
          boundingBox = Geometries.rectangle(minX, minY, maxX, maxY);
          System.out.println("Bounding Box: " + boundingBox);
      }
  
      public boolean isInside(Point p) {
          // 先判断点是否在最小外包矩形内
          if (!boundingBox.contains(p.getLon(), p.getLat())) {
              return false;
          }
  
          // 为了获取可能相交的边，将查询矩形扩大一定的范围
          Rectangle searchRect = Geometries.rectangle(Geometries.point(p.getLon(),p.getLat()));
          Integet count = rTree.search(searchRect).map(Entry::value)
                  // 粗筛后使用反射法
                  .map(fence -> isRayIntersectsSegment(p.getLat(), p.getLon(), fence))
                  .count().toBlocking();
          return (count % 2) == 1; // 奇数表示在多边形内
      }
  
      private List<Edge> createEdgesFromVertices(List<Point> vertices) {
          List<Edge> edges = new ArrayList<>();
          for (int i = 0; i < vertices.size(); i++) {
              Point start = vertices.get(i);
              Point end = vertices.get((i + 1) % vertices.size());
              edges.add(new Edge(start.getLon(), start.getLat(), end.getLon(), end.getLat()));
          }
          return edges;
      }
  
      public boolean isRayIntersectsSegment(double lat, double lon, Edge edge) {
          double x1 = edge.x1;
          double y1 = edge.y1;
          double x2 = edge.x2;
          double y2 = edge.y2;
  
          System.out.println("Checking intersection with edge: " + edge);
  
          // 边平行于x轴，不相交
          if (y1 == y2) return false;
  
          // 点在边的上方或下方，不相交
          if (y1 > lat && y2 > lat) return false;
          if (y1 < lat && y2 < lat) return false;
  
          // 点在边的上方（冗余检查）
          if (Math.max(y1, y2) < lat) return false;
  
          // 计算交点
          double xIntersect = x1 + (lat - y1) * (x2 - x1) / (y2 - y1);
  
          // 检查是否相交 (包括等于的情况)
          boolean intersects = xIntersect >= lon;
          System.out.println("xIntersect: " + xIntersect + ", lon: " + lon + ", intersects: " + intersects);
          return intersects;
      }
  }

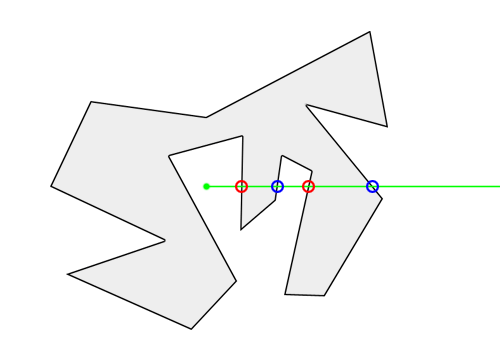
Q:大多数应用的地理围栏多边形都比较简单，但有时也会遇到一些特别复杂的多边形，比如单个多边形的边数就超过十几万条，这时候对此复杂多边形执行一次射线法也非常耗时（因为射线法时间复杂度为O(N)，N为多边形边数），这种怎么处理。
A:首先对多边形的每条边构建最小外包矩形，然后在这些最小外包矩形基础上构建R树索引（R树索引上的外包矩形未画出），这样射线法求交点的时候首先通过R树判断射线是否与外包矩形相交，最后对R树粗筛后的边进行精确求交判断，时间复杂度从O(N)降到O(Log(N))，大大提高了计算效率。

总结

基于RTree 实现空间数据的索引，结合射线法进行细粒度判断，即可以大幅提升查询效率，也保证了算法的准确性，极其适用于大规模空间数据的管理和查询。但也存在一些弊端：

RTree 结构和射线法结合实现起来相对复杂，需要处理多种边界情况，导致复杂性较大。

RTree 需要存储大量的节点信息，对于大规模数据可能带来较大的存储开销

参考文献

CSDN

射线法-判断一个点是否在多边形内部

博客园

地理围栏算法解析

知乎

数据结构之R Tree

CSDN

回转数法-判断一个点是否在多边形内部